毎月支払額と利率から「現在価値」を「一発で」求める方法

Hagiyamaです。

IFRSにおいても株価の価値評価（バリュエーション）においても、「現在価値」については避けては通れない考え方です。

現在価値の基本的な考え方についてはインターネット上で溢れていますので（現在持っている１万円と将来の１万円は価値が違う等）、それらのウェブサイトに説明を譲るとして、、

ここでは巷の現在価値の考え方とは少し違った角度から、現在価値について検討したいと思います。

【設例】
リース料を毎月10万円を支払い、その年利率は２％とする。
これを５年間（60カ月）継続するとした場合、リース資産の現在価値はいくらになるか？

IFRS16号（リース）などで出てきそうな考え方ですが、これは借入金や社債などの負債性の金融商品などにも応用できる考え方です。

リース資産の現在価値を算出する際に、返済予定表から毎月の支払額についての元本と利率と算出するという方法が一般的には行われています。

その場合は、60か月分の返済スケジュールから現在価値を算出することになるため、計算が多くなり少し煩雑となります。

実は、リース資産の現在価値を一発で計算できる方法があります。

これには、PMT（Payment）という考え方を利用します。

エクセルにはPMT関数がありますが、これは利率が一定と仮定した場合の元利均等の毎月支払額を計算する関数です。

そのため、【設例】のような現在価値を求めるという場合には、残念ながらPMT関数を使っても求めることはできません。

現在価値を一発で求めるには、PMTの考え方を利用して、手入力で数式を計算する必要があります。

下記に、私が作成した【設例】に関するエクセルの部分キャプチャを貼り付けます。

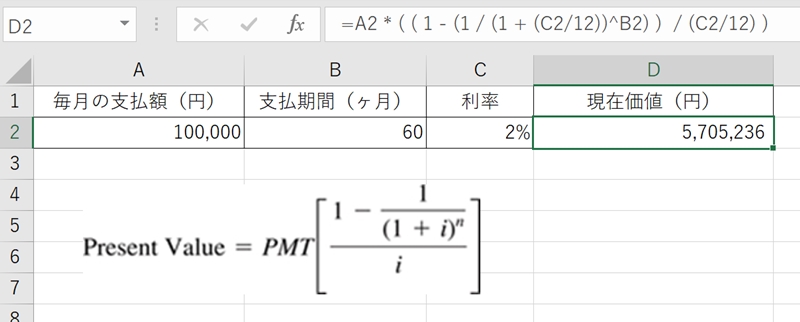
D2セルに答えとなる現在価値の数式をPresent Valueの公式に基づき入力していますが、毎月払いですので年利率を12で割って計算しています。

これにより、毎月１０万円を５年間、年利率２％で支払う場合の現在価値は、5,705,236円と算出できました。
毎月の支払額（A2セル）や支払期間（B2セル）、利率（C3セル）の数値を変えれば、他の条件でも対応ができます。

こういった数学的な考え方を知っておくと、何かと便利なことがあります。

「数学なんて普段の生活で使わないから勉強する必要はない」といった考えがありますが、数学は知らないよりかは知っているほうが遥かに有利になる学問だと思います（もちろんこれは数学に限った話ではありませんが..数学の必要性については、下記の記事でも述べています）